Red-black trees (part 5, bis)

published: Sat, 3-May-2008   |   updated: Sat, 20-Aug-2016

Something that occurred to me after I'd posted part 5 in my red-black tree series is that I was relying on you, the reader, visualizing the rotations and recolorings in my insertion example. I should have shown each intermediate step for each insertion, rather than just the end result. Doing so would have helped you picture the changes that are happening during this process.

Well, no problem, I've quickly modified the code to take a snapshot after each rotation and recoloring to help you see what's going on. I'll use the same example as before; that is, inserting p, g, w, s, c, u in that order into an empty red-black tree. You'll see the main cases (but not necessarily their mirror versions).

First up is inserting p.

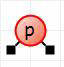
Inserting p as red root

It's added as a red node, and as the root.

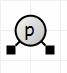
Recoloring p to black

Immediately, though, we force it black. That's the final step of inserting p.

Next up is inserting g.

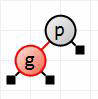
Inserting g as red node p

It goes to the left of p since it is less than it, and it will be colored red. There are no color fixups to do. This is the end-result of adding g.

Next, insert w.

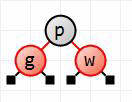
Inserting w as red node

It's greater than p and so goes to p's right. It's red by default, and there are no other color fixups to make. This is the end-result of adding w.

Next, insert s.

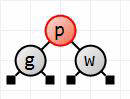
Recolor p, g, and w to avoid red siblings

First step here is to recolor p, g, and w, since they form the black-parent-two-red-children scenario.

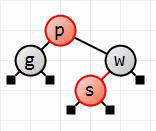
Add s a red node

We find where to place s (to the left of w) and it will be red of course.

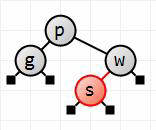
Recoloring p to black

On return from the insertion, we force p's color to be black again. This is the end-result of adding s.

Next, insert c.

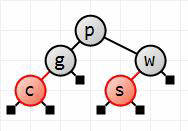
Inserting c as red node

It'll end up as the left (red) child of g. No color fixups are needed. This is the end-result of adding s.

Next insert u. This is the interesting case in our example.

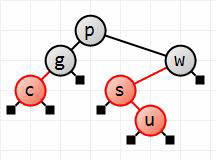
Add u as red node

We follow the path down and insert it as a red child of s, on its right. This gives us case B: u is a right child of s, which is a left child of w.

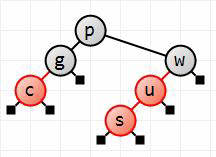
Rotate s left, bringing up u

We first rotate s left, bringing up u, giving us case A (w's left child is u, and u's left child is s).

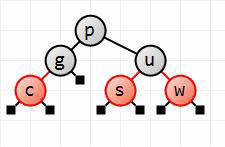
Rotate w right and recolor u and w

Now we rotate w right and recolor u and w to give the fixed red-black tree shown. This is the end-result of adding u.

There, I hope that helps a little more than before.

[This is an addendum to part 5 of a series of posts on red-black trees. Part 1. Part 2. Part 3. Part 4. Part 5. Enjoy.]