Red-black trees (part 5)
published: Sat, 26-Apr-2008 | updated: Sat, 3-Nov-2018
In our previous installment, we'd introduced the principles behind red-black trees as well as an appreciation of why they would produce more balanced binary search trees than pure randomness by using a process called a rotation. Then we got stuck when actually inserting a node. Obviously this is one algorithm we are going to have to crack in order to be able to build a red-black tree that we can search.
To recap, we determined that it was best to attach a new node as a red node — since making it a black node would automatically and immediately violate rule 4: "For every node in the tree, each path starting at that node to an external node has the same number of black nodes." But, having said that, we then determined that we could sometimes violate rule 3: "If a node is red, both its children are black" if the parent of the new node happened to be red too.
Our brief observations last time showed us that there were two main cases to fix up. These two cases have mirror images, making four possible cases in all. Let's call them A and A' (A-prime), and B and B'.
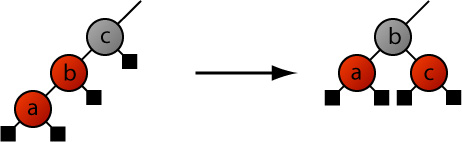
With A we have the new node attached as a left child of a red parent that is itself a left child, and its mirror image A' having the new node as a right child of a parent that is a right child. This is the easy case we solved last time: we merely rotate the parent about its parent and recolor them both. We noted that the sibling of the parent had to be black for this to work.
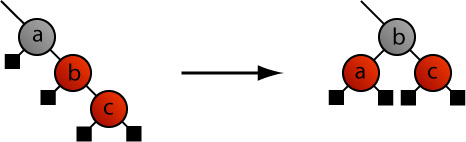
The other two mirrored cases, B and B', gave us pause, but in reality are as simple to solve as the first two cases. We merely have to do two rotations instead of one. (Authors usually call this a zig-zag rotation since we rotate first in one direction and then in the other direction.) The B case here is the new node is the right child of a parent that is a left child; with the mirror case, B', having the new node as a left child of a right facing parent.
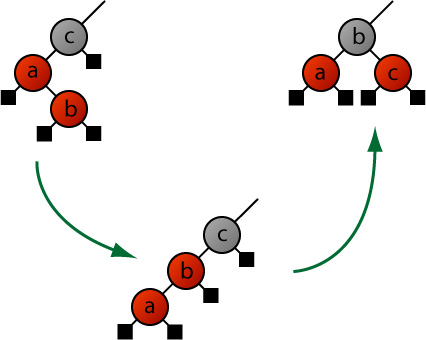
Taking case B (a right child of a left parent), we initially rotate the parent left (anticlockwise), bringing the new node up. If you look at this intermediate stage you can see that it is exactly our first case A. And we know how to fix that: rotate the new node with its new parent and recolor. Score!
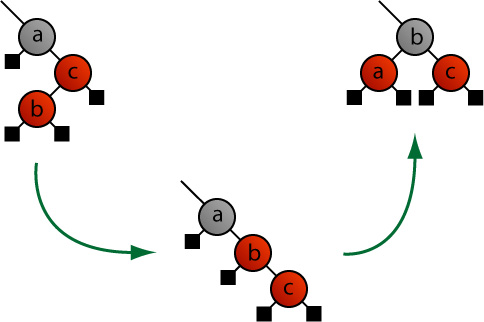
B' is equally easy to fix: rotate the parent right, bringing up the new node — giving us the easy case — and then rotate its new parent left and recolor.
The big fly in the ointment is what to do when the sibling of a red node is also red. For, no matter what we do, if we carry out these rotations, we will end up with two reds in a row and that's a firm violation of rule 3.
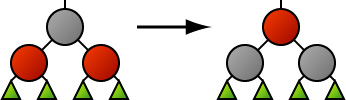
By far the easiest solution to this problem is perhaps a little counterintuitive. We just get rid of these cases (that is, black parent with two red children) as we move down the tree trying to find the place to insert the new node. How do we do that? This has to be the simplest fix of all: we merely recolor the parent of the two red children red, and its two children black. That way, when we get to the point when we insert the new node, there won't be any node-with-two- red-children situations above us in the tree. We can rotate with impunity.
There is a small gotcha, unfortunately. In making these quick "destroy all red children pairs" operations as we go down the tree, we may leave behind some red nodes with red children (after all we are, in a way, moving the "redness" attribute up the tree in destroying these red children pairs and may inadvertently force a red parent to have a red child). No matter, we will return back up the tree and fix them after we've inserted a new node and doing any necessary rotations that insertion required.
How do we do that, you may ask. Surely that would involve having parent pointers for each node? Or maybe we'll have to push visited nodes onto a stack so that we can travel back up the tree by popping off nodes?
No, no, nothing so complicated. We merely implement insertion using a recursive method, instead of an iterative method as we did with a simple binary search tree. When we regain control after making a recursive call we patch up the part of the tree we can see from this vantage point (if needed, of course) before returning.
There is one more little hack we'll make use of: if the root of the tree is colored red after completing the insertion of a new node, we can make it black without causing any violations of the rules. This simple change can make our lives easier when we perform insertions, but it doesn't have the force of an actual rule.
Now when I started writing this code it got very ugly very quickly.
The reason was that I now had two layers of implementation inheritance
(IBinaryNode -> BsTreeNode ->
RedBlackNode) and I was starting to write an awful lot of
code that cast a node to a descendant. Because the latter two types in
the chain were generic I was getting really tired of typing angle
brackets. So a revamp of the code was in order.
(Unfortunately, this also means that my grand plan of having VB code as well as the C# code is going to be put on hiatus for a while. This installment is, shall we say, a little late, and I don't have the time to keep up the maintenance of the VB code as quickly as the C# code. I'll redo it when I get to the next stage and have time. Also, from my web stats I see that about 15 times more people download the C# code than the VB code. So please bear with me.)
First thing is a node for the red-black tree. Originally I had this
descend from the BSTreeNode, but that was getting too
awkward and so I just made it an implementation of the
IBinaryNode interface directly.
public class RedBlackNode<K, V> : IBinaryNode where K : IComparable<K> { private bool isBlack; private K key; private V value; private RedBlackNode<K, V> left; private RedBlackNode<K, V> right; public RedBlackNode(K key, V value) { this.key = key; this.value = value; isBlack = false; } public RedBlackNode<K, V> RotateLeft() { var temp = this.Right; this.Right = temp.Left; temp.Left = this; return temp; } public RedBlackNode<K, V> RotateRight() { var temp = this.Left; this.Left = temp.Right; temp.Right = this; return temp; } public RedBlackNode<K, V> Advance(K key) { int compareResult = key.CompareTo(Key); if (compareResult == 0) return this; if (compareResult < 0) return Left; return Right; } public K Key { get { return key; } } public V Value { get { return value; } set { this.value = value; } } public bool IsBlack { get { return isBlack; } } public bool IsRed { get { return !isBlack; } } public void MakeBlack() { isBlack = true; } public void MakeRed() { isBlack = false; } public RedBlackNode<K, V> Left { get { return left; } set { left = value; } } public RedBlackNode<K, V> Right { get { return right; } set { right = value; } } IBinaryNode IBinaryNode.Left { get { return this.Left; } set { this.Left = value as RedBlackNode<K, V>; } } IBinaryNode IBinaryNode.Right { get { return this.Right; } set { this.Right = value as RedBlackNode<K, V>; } } }
As you can see from the constructor, red-black nodes are created red
by default, which goes along with the first basic step of the
insertion algorithm. Next in line are the two rotation methods:
RotateLeft() and RotateRight(). These will
be called on a particular node by the red-black tree, and return the
new parent of the node after rotation. Both methods make the
assumption that the child node being promoted is not an external node,
and, as you'll see, the red-black tree will make sure this contract is
valid.
At the end of the code, you'll see that I'm providing both implicit
and explicit implementations of IBinaryNode's methods.
Again this is to save on casts: I'll be using Left and
Right a lot and don't want to continually cast to the
RedBlackNode<K,V> type.
public class RedBlackTree<K, V> : IBinarySearchTree<K, V> where K : IComparable<K> { private RedBlackNode<K, V> root; public static bool IsRed(RedBlackNode<K, V> node) { return (node != null) && node.IsRed; } public void Insert(K key, V value) { Root = Insert(Root, key, value, false); Root.MakeBlack(); } public RedBlackNode<K, V> Root { get { return root; } set { root = value; } } IBinaryNode IBinarySearchTree<K, V>.Root { get { return this.Root; } set { this.Root = value as RedBlackNode<K, V>; } } public bool Contains(K key) { return GetNode(key) != null; } public RedBlackNode<K, V> GetNode(K key) { var walker = root; while (walker != null) { var nextNode = walker.Advance(key); if (nextNode == walker) return nextNode; walker = nextNode; } return null; } public bool TryGetValue(K key, out V value) { var node = GetNode(key); if (node == null) { value = default(V); return false; } value = node.Value; return true; } public V this[K key] { get { var node = GetNode(key); if (node == null) throw new Exception("Red-black Tree: Key not found using indexer"); return node.Value; } set { var node = GetNode(key); if (node == null) Insert(key, value); else node.Value = value; } } }
Now onto the red-black tree itself (most of the code above merely
supports the standard methods like Contains() and so on)
and the Insert() method. This is quite simple since we
make use of an overloaded method to do the actual work. On return from
this call, we make the root node black.
The real Insert() method is recursive, although it's a
method it calls that makes the recursive call. This method takes a
current node value (where we are in the tree), the key and value, and
an indicator that reveals whether this current node is to the left or
the right of its parent. (For the root node, we can pass whatever we
like for this value, since it doesn't have a parent. I've assumed that
the root lies to left of its invisible parent.) The method returns a
node so that it can be attached as the left or right child of the
current node's parent.
private RedBlackNode<K, V> Insert(RedBlackNode<K, V> current, K key, V value, bool currentIsRightChild) {
// if we're at an external node, return a new red node
if (current == null)
return new RedBlackNode<K, V>(key, value);
// if both our children are red, recolor us and them
if (IsRed(current.Left) && IsRed(current.Right)) {
current.MakeRed();
current.Left.MakeBlack();
current.Right.MakeBlack();
}
// Check for inserting on the left or the right
int compareResult = key.CompareTo(current.Key);
if (compareResult == 0)
current.Value = value;
else if (compareResult < 0)
current = InsertOnLeft(current, key, value, currentIsRightChild);
else
current = InsertOnRight(current, key, value, currentIsRightChild);
return current;
}
First up in the Insert() method is to see if the node
we're at is an external node. If it is we return a new red node
containing the key and value.
If the current node is not an external node, we then check to see if it's black and its two children are red. If so, we immediately recolor all three nodes. To check that a node is red in this method, we have to be somewhat careful. Remember that external nodes for the tree are null and so we can't just get a reference to a node and check its IsRed property: we may throw a null reference exception. The best bet is to create a simple static method of the tree that does the proper check against null (in which case the node is black) before dereferencing the object to find out what color the actual node is. This is the IsRed() static method, shown in the code for the tree. (Also note that if this method returns true, the node is not null. This corollary is assumed at a couple of points in the remaining code.)
Now we get to the point where we need to recurse. We compare the key we're inserting against the current node. If equal we set the current node's value to the value passed in. This is different from before where I threw an exception if you were trying to insert a key that already existed in the tree. This mimics the convention that the .NET Framework uses for its hashtable and dictionaries: if the key exists, replace thr value associated with it.
Otherwise we have to insert the key/value pair to the left or to the
right. These two options are merely the mirror images of each other
and so I'll only discuss the left variant,
InsertOnLeft().
private RedBlackNode<K, V> InsertOnLeft(RedBlackNode<K, V> current, K key, V value, bool currentIsRightChild) {
current.Left = Insert(current.Left, key, value, false);
if (IsRed(current) && IsRed(current.Left) && currentIsRightChild)
current = current.RotateRight();
if (IsRed(current.Left) && IsRed(current.Left.Left)) {
current = current.RotateRight();
current.MakeBlack();
current.Right.MakeRed();
}
return current;
}
private RedBlackNode<K, V> InsertOnRight(RedBlackNode<K, V> current, K key, V value, bool currentIsRightChild) {
current.Right = Insert(current.Right, key, value, true);
if (IsRed(current) && IsRed(current.Right) && !currentIsRightChild)
current = current.RotateLeft();
if (IsRed(current.Right) && IsRed(current.Right.Right)) {
current = current.RotateLeft();
current.MakeBlack();
current.Left.MakeRed();
}
return current;
}
The first thing we do is to recursively call the Insert()
method on the current node's left child. On return from that recursive
call we set the left child, and then we check for two possible
red-node violations. The first such is to see whether we can do the first
rotation of case B above. That is, the current node is red, it's a
right child, and its left child is red. In this case, we rotate the
current node right — the first step of solving case B. The second
step of case B is going to be done by the recursive step of current's
parent. Note that we don't have to worry about dereferencing an
external node (which is usually null): red nodes are always internal
nodes, never external.
Now we check to see if the left child and its left child are both red. This is the main scenario for case A, and is the second step for case B. If so, we do the rotation (rotating the current node right) and fix up the colors. Again, there are no possible null node dereferences since red nodes are never null.
For the final step we return the (possibly changed) current node.
And, that, believe it or not, is the insertion algorithm for red-black trees.
Let's add a series of nodes to a red-black tree so that you can see the processes involved. I'll add the same nodes as I did for the ordinary binary search tree, in the same order. For practice, it would be instrumental if you checked that the various red-black rules are satisfied at the end of each insertion.
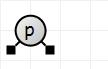
We first insert p. Since the tree is empty, a new red node is inserted as the root. On return from the insertion code, we force the root to be black.
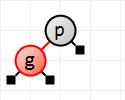
We now insert g. It goes to the left of p since it is less than it, and it will be colored red. There are no color fixups to do.
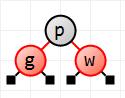
Now w. It's greater than p and so goes to p's right. It's red by default, and there are no other color fixups to make.
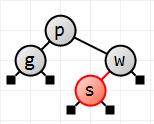
Now s. In finding where to insert s, we immediately notice that we have a black parent with two red children, and so we recolor them. p is now red and g and w black. We find where to place s (to the left of w) and it will be red of course. On return from the insertion, we force p's color to be black again.
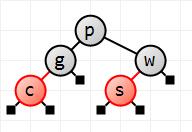
Next up is c. It'll end up as the left (red) child of g. No color fixups are needed
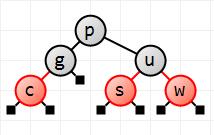
Next is inserting u. We follow the path down and insert it as a red child of s, on its right. This gives us case B above: u is a right child of s, which is a left child of w. We first rotate s left, bringing up u, giving us case A (w's left child is u, and u's left child is s). Now we rotate w right and recolor u and w to give the fixed red-black tree shown. This step produces a much more balanced tree than the 6th step of the binary search tree exmaple.
(For a step-by-step view of the rotations and recolorings in this example set of insertions, see this post.)
As with any recursive algorithm we have to worry about runaway recursion and possible stack exhaustion. Since the whole purpose of the red-black tree is to create a reasonably well-balanced tree, and a balanced tree has depth proportion to the logarithm of the number of entries, and the maximum path in a red-black tree is twice the shortest, we can say without too much mathematics that the number of recursive calls will be at most 2*log(n). For 1 million items (2^20 items) that means we would have, at maximum, 40 recursive calls and generally much less than that. This is hardly a runaway recursion.
Next time we'll think about deletion and decide it's all too complicated.
[This is part 5 of a series of posts on red-black trees. Part 1. Part 2. Part 3. Part 4. Enjoy.]
