PCPlus: Cyclomatic Complexity
published: Tue, 17-Jun-2008 | updated: Fri, 5-Aug-2016
(Back at the beginning of 2007, I signed up to write a monthly column called Theory Workshop for PCPlus in England. Part of the sgreement was permission to republish the articles on my website once a reasonable length of time had passed. Here's the second of those articles. It was originally published in issue 256 of PCPlus, dated June 2007. Note that with these reprints I may extend the original article with example code, but in general I won't be rewriting them. I'll also drop the strap and intro, since they're more specific for the mag and don't make much sense here.)
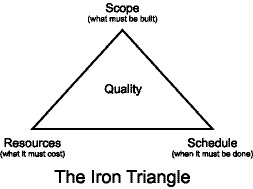
There's an old programming joke, based, as many jokes are, in reality, where a programming team lead is asked about the quality of a project and says, scope, schedule, cost: choose two. In other words, if you want a quality project completed in a certain time with a given scope (scope meaning features), you are forced to accept whatever cost it takes, otherwise the quality will suffer. This abstraction is known as the Iron Triangle.
We can easily define the quality of a complete application like this: it works as expected; it doesn't crash; it doesn't corrupt its data; and so on. We could also propose the elegance of the program's interface, the discoverability of its features, and the speed of its operation as being important components of its quality, but it's all very subjective.
Iron Triangle. A software development project has conflicting goals: scope (what must be built), resources (what it must cost), and schedule (when it must be done by). These are usually drawn as a triangle, which represents the quality of the project. Fix any two of the goals and the third must be fixed as well to maintain the quality of the completed project. Similarly, reduce any of the goals and you must correspondingly decrease the others to maintain the same level of quality. The triangle, if you like, is rigid, made of iron; you can't stretch it. By educating the stakeholders of the project in this metaphor, you can avoid some of the problems that make projects late or that exceed the project's budget.
For the actual lines of code the programmer writes, we'd like to be more objective. How can we define the quality of some block of code?
Back in the 60s and 70s, this question resulted in quite a bit of research. The initial assumption was that we should be able to "measure" our code in some way to produce a simple numerical value. With this we can make comparisons and argue about the meaning of larger or smaller values. This research resulted in a new branch of software engineering called software metrics.
The easiest measurements to make are related to the "size" of your program. Simple ones include the size in bytes of the compiled program on disk, the number of lines of code, the number of tokens in the source code, and so on. These size measurements are important for a few reasons: they're easy to calculate, they result in simple numerical values, and they are often used as measurements of productivity of a programmer.
The number of lines of code or LOC is a popular measurement. Back in the old days of programming on punched cards, this translated to the weight of the deck of cards for your program; the heavier the deck, the more lines of code. Or, if you like, it translated to the length of time it took to reorder the cards if you were unlucky enough to drop the deck onto the floor.
Of course, this is also equivalent to counting the number of line endings in a text file, but, no matter how you do it, LOC is very unsatisfactory. Blank lines and comments will count towards the total, yet by no stretch of the imagination can these be called lines of code. Nowadays, the LOC measurement does not include these, but there is some debate on how to deal with code statements that span several lines. In Visual Basic, for example, it's very obvious when a code statement spans several lines (there's a line continuation character), but in SQL procedures, it's not.
There's another problem with LOC that's not quite so obvious: some lines of code are easier to write than others. For example, incrementing an integer variable is a very easy statement to write, however writing the initial statement for a counting loop (a for loop) is more complicated since you have to consider whether the counter has been defined, the bounds of the loop, the syntax of the statement, whether you are counting up or down, and so on.
LOC then does not take into account the complexity of code, so a refinement has been to calculate the number of tokens in the code. For example, in the C languages, incrementing a variable called i is achieved by i++;, with three tokens present (i, ++, and ;). If you calculate the total number of tokens in a program and divide it by the number of lines, you'll get a measurement that describes the complexity of the code. The higher the tokens/line value is, the more complex the code; the lower the value, the simpler the code.
Since the quality of our code is related to our ability as programmers to understand it, writing complex code is more likely to result in lower quality code than writing simpler code. If we understand it, we're more able to decide whether the code works as is and whether it contains bugs.
Unfortunately, the tokens/line measurement is very dependent on the programming language being used. Terse languages will have different tokens/line measurements than verbose languages when implementing the same algorithm. We need a better measurement, one that is language- independent, so we can draw conclusions about quality without having to qualify them with the language being used.
In 1976, Thomas J. McCabe came up with such a measurement and called it cyclomatic complexity, or CC. It is a description of the complexity of the control flow of a program. To put it another way, it's a numerical description of the complexity of a flowchart: the more decision boxes in a flowchart, the more complex the control flow.
By analyzing many software projects, both before and after the software was released, he showed that the reliability of a program, and hence quality, is inversely correlated to its control flow complexity and the number of errors a program exhibits is directly correlated to it. In other words, the more complex a program is, the less reliable it is and the more errors show up after it's released.
Combining CC values.
Suppose you have one routine (call it A) that calls another (called
B), what is the overall cyclomatic complexity of this subsystem?
Routine A needs one extra arrow to go to B (the call) and one extra
arrow to come back (the return). Using McCabe's formula CC = E - N + 2
for both routines and noticing that the new extra arrows on A are the
entry/exit arrows for B, so we don't count them twice, the total
number of edges is the sum of the edges in A and in B plus 2, the
total number of nodes is the sum of those in A and in B, and so we
get:
SumCC
= (EA + EB + 2) - (NA + NB) + 2
= (EA - NA + 2) + (EB - NB + 2)
= CCA + CCB
Hence, the cyclomatic complexity of a subsystem is the sum of the
complexities of its parts.
McCabe's initial research has been confirmed in later years by other researchers. His findings have been extended by additional measurements (for example, adding in the number of local variables), but the CC metric is still an extremely good indicator of the quality of a program. If we write programs with a low CC value we'll be less likely to write buggy ones.
McCabe not only showed that programs with a low CC value are more reliable, but also showed how to calculate the overall CC by combining the CC from the individual routines or methods in the program. Further research has shown optimal values for the CC for a method or routine, meaning that you can improve the CC of the entire program by concentrating on the CC for individual routines.
Here's McCabe's algorithm for calculating the cyclomatic complexity of a method or routine:
- Start with 1. All this says is that, if called, the method will finish; there is at least one path through the method.
- Add 1 for each conditional statement or looping statement. (So, add 1 for an if, or a while, or a foreach, or a ternary operator, etc.)
- Add 1 for each AND or OR logical operator used in a condition.
- Add 1 for each case block in a select or switch statement. If the switch statement doesn't have an explicit default case block, add 1.
- Add 1 for each catch statement for a thrown exception (in Delphi this is the except statement).
After this calculation you'll get a value that's at least 1. If it is exactly 1, then the CC value shows the method is merely a sequence of one or more statements. Between 2 and 5, you shouldn't worry particularly about the method: it's not that complex. If the value were between 6 and 10, I'd have to say it's getting a little too complex to understand in one go. Any method that has a CC value of 10 or more is definitely too complex and should be refactored.
Put it another way: the CC value is a measure of the number of paths through the method and so indicates at least the number of tests you need to make to properly exercise the method. So a method of complexity 10 will require, at a minimum, 10 tests to ensure that all paths are checked. The more testing coverage you have, the higher the quality of the code.
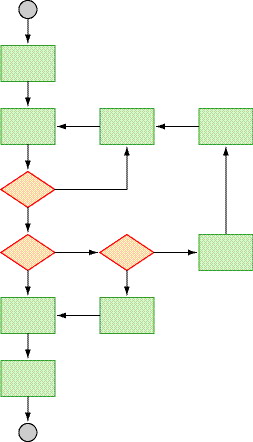
In conclusion, for code that is to be maintained and enhanced over a period of time, you should pay attention to its quality, and the easiest way to check for that is by using McCabe's cyclomatic complexity.
Flowchart logic complexity
McCabe's insight is that it is the number of decision points that defines the complexity of the code. The more decision points there are, the more bugs can be inadvertently introduced. The way he described the calculation for a method was in terms of the flowchart of the method. Count the number of edges (arrows), the number of nodes (boxes), subtract the latter from the former and add two (one for the arrow to enter the flow chart and one for the exit). The formula for the cyclomatic complexity is CC = E - N + 2.
For the flowchart shown, the number of arrows is 13, the number of boxes is 11, and so the CC value is 4.
The interesting thing about this formula is that, if you split a non- decision box into two boxes connected by an arrow (or combine two connected non-decision boxes), you don't change the CC value. You can simplify it even further: if you just count the number of decision boxes and add 1, you get the CC value.
