Kruskal's Algorithm
published: Sat, 8-Jul-2006 | updated: Sat, 6-Aug-2016
I noted recently that has been some time since I last blogged here about an algorithm. I do apologize. It's unfortunate, but I can only give the same old excuse as any other tech blogger: sometimes work overpowers everything and writing an algorithm article sometimes can take a little while. Anyway, having offered an apology (which I hope was accepted), let's dive straight into one I've not used before, one of a set that deals with graph data structures.
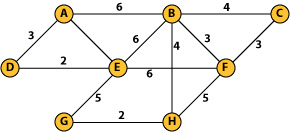
Imagine we have an undirected connected graph where the edges connecting the vertexes have weights associated with them. I'm sure you're familiar with Dijkstra's Algorithm that tries to find the minimum weighted path from a given vertex or node to another. Alongside that algorithm lies Kruskal's Algorithm which returns the minimum spanning tree of all the vertexes; that is, the tree containing all the nodes that has the minimum total weight of the edges.
One of my former colleagues (I almost said "one of my old colleagues" just then, but she wouldn't have been happy about that, quite understandably) asked me about this algorithm recently, saying that the references on the internet weren't easy to understand or to implement. So I said I'd help out.
In essence Kruskal's Algorithm goes like this (here's the wikipedia reference):
Add all the vertexes to a forest. Find the smallest edge (that is, the edge with the smallest weight). Unless the edge forms a closed loop, find the two trees in the forest that contain the end-point vertexes for the edge and join them. Find the next smallest edge and repeat. Once you've gone through all the edges, you should have a single tree in the forest: it is this tree that is the minimal spanning tree.
Now, this brief explanation leaves a lot out, as my friend found. What data structures should we use? How do you tell that there's a closed loop? How do we represent the minimal-spanning tree? And so on.
Let's take it slowly, piece by piece.
First we'll need a Vertex class. Not too sure yet, what we'll
include as behavior or attributes yet, so let's just leave it bare.
public class Vertex {
public Vertex() {
}
}
Next we need an Edge class. Here the attributes are more well
defined: there's a weight value, and there are two vertex references for the
vertexes at the end of the edge. The only behavior that I can see at this point
is that edges should be comparable by weight: I will need to say whether one
edge's weight is smaller or greater than another's.
public class Edge : IComparable {
private int weight;
private Vertex left;
private Vertex right;
public Edge(int weight, Vertex left, Vertex right) {
this.weight = weight;
this.left = left;
this.right = right;
}
public int CompareTo(object obj) {
Edge e = obj as Edge;
if (obj == null)
throw new ArgumentNullException(
"Edge.CompareTo() passed invalid or null object");
if (this.weight < e.weight)
return -1;
if (this.weight > e.weight)
return 1;
return 0;
}
}
Now we need a container for a set of edges. This container must have the functionality that we can add an edge to it (so that we can initially populate it) and then have an iterator on it (so that we can retrieve the edges in ascending order of weight).
Originally, I thought of using a priority queue, but my friend pointed out that that was probably overkill: a simple sorted array would do just fine. She was right since we have no need of a random set of additions and removals: all we will be doing is adding all the edges in one fell swoop in sorted order by weight and then iterating through them one at a time.
public class OrderedEdgeList : IEnumerable {
List<Edge> list = new List<Edge>();
private int GetInsertionPoint(Edge item) {
int l = 0;
int r = list.Count - 1;
while (l <= r) {
int m = l + (r - l) / 2;
int compareResult = list[m].CompareTo(item);
if (compareResult < 0)
l = m + 1;
else if (compareResult > 0)
r = m - 1;
else
return m;
}
return l;
}
public void Add(Edge item) {
list.Insert(GetInsertionPoint(item), item);
}
public IEnumerator GetEnumerator() {
return list.GetEnumerator();
}
}
How about the representation of the minimum-spanning tree? This is where it gets interesting, since there are two ways of looking at it. You could be literal and represent the minimum-spanning tree as, well, you know, a tree. In other words, there'll be a root (some vertex), and each node in the tree is a vertex with zero or more children vertexes. Not a binary tree, since we're not limiting the number of edges from a vertex to three (one parent and two children), but a more general n-ary tree.
Or you could be less literal and just return a list of the edges that participate in the minimum-spanning tree. From that, the caller of the algorithm can decide to build an actual tree or do something completely different; after all, he will have all of the information required. Passing back a tree is less optimal in that we will have to somehow incorporate the edges (and their weights) into it.
We'll do the second option: we will return a list of edges that participate in the solution to the minimum-spanning tree.
After this we have the problem of the forest to solve. A forest is merely a collection of trees (well, d'oh!), so some kind of unordered list will do just fine. But what is a tree in this definition? Again, let's not be literal, but instead define a tree as simply a list of vertexes that are connected by edges we've already seen.
When we initially populate the forest with vertexes, we'll morph each vertex into its own tree. When we pick out the first edge (defining a link between two vertexes), we'll find the trees containing these vertexes in the forest, remove them both, "join" the two trees into one, and add the resulting (bigger) tree back into the forest.
But what happens if both vertexes from our current smallest edge are in the same tree? Well, if you think about it, it would mean that the edge would produce a closed loop (ah ha!), so we would discard the edge.
So a tree in our forest just contains a set of vertexes, with the ability to say whether a vertex is part of it, and with the ability to join itself onto another tree (that is, add all of its vertexes to the other tree). We do not have to work out or maintain parent and children links in this "tree". Cool.
Implementing "join" is fairly easy (just cycle through all the vertexes in the smaller tree and add them to the larger one, discard the smaller tree), and indeed I can't think of simpler way to do it, but how to find out which tree a vertex is in? We could cycle through all the vertexes in a tree and check each to be the one we want, but that seems long-winded. Is there not a way to simply check whether vertex V is in tree T? Yes, of course there is, we just store a link to the tree inside the vertex (call it the vertex' tree parent, if you like). (That does mean that when we join a tree to another, we not only have to add all the vertexes to the other tree, we also have to update the tree parent links.
OK, time for some more code, methinks. First, we'll jazz up the
Vertex class a bit so that we can maintain a link to the parent
tree, give it a name, and also create a linked list of vertexes:
public class Vertex {
private Tree treeParent;
private Vertex next;
private string name;
public Vertex(string name) {
this.name = name;
}
public override string ToString() {
return name;
}
public Tree TreeParent {
get { return treeParent; }
set { treeParent = value; }
}
public Vertex Next {
get { return next; }
set { next = value; }
}
}
Edge class:
public class Edge : IComparable {
...same as before...
public override string ToString() {
return String.Format(
"Edge from {0} to {1} (weight: {2})",
left, right, weight);
}
public Vertex Left {
get { return left; }
}
public Vertex Right {
get { return right; }
}
}
Tree class:
public class Tree {
private int count;
private Vertex root;
public Tree(Vertex root) {
this.root = root;
this.count = 1;
root.TreeParent = this;
}
public bool Contains(Vertex vertex) {
return vertex.TreeParent == this;
}
public void Add(Vertex vertex) {
vertex.TreeParent = this;
vertex.Next = root;
root = vertex;
count++;
}
public Tree Join(Tree tree) {
if (count < tree.count)
return tree.Join(this);
Vertex walker = tree.root;
while (walker != null) {
Vertex next = walker.Next;
Add(walker);
walker = next;
}
return this;
}
}
There are several things to notice here. The tree is in fact implemented as a
linked list of vertexes. The root field points to the first item
(vertex) in the linked list and we also maintain a count of items
in the list (this will help us in a moment when we talk about the join
operation). The constructor for the tree accepts a vertex (all vertexes are
added to the forest as trees, remember) and sets the vertex'
TreeParent property to itself. The Contains() method
is really simple: it just checks that the given vertex' tree parent is this
one.
Look at Join() now. It makes sense to join the smaller tree to the
larger, and this is what the first if statement is doing. Otherwise we would
continue by walking along the other tree's linked list, adding each vertex
encountered to ourselves. The adding is done via the Add() method,
which merely adds the new vertex to the beginning of the linked list. We
remember to set the tree parent as well, of course.
Now for the Forest class:
public class Forest {
private List<Tree> list = new List<Tree>();
public void Add(Tree tree) {
list.Add(tree);
}
public void AddVertex(Vertex vertex) {
Add(new Tree(vertex));
}
public Tree Find(Vertex vertex) {
foreach (Tree tree in list) {
if (tree.Contains(vertex)) {
return tree;
}
}
throw new ArgumentException("Vertex not found in forest");
}
public void Remove(Tree tree) {
list.Remove(tree);
}
}
Nothing much to see here; it's all very simple.
Now for the actual code for Kruskal's algorithm, which I cheated a bit and wrote as a console application to solve the above graph:
class Program {
static void Main(string[] args) {
Forest forest = new Forest();
OrderedEdgeList edges = new OrderedEdgeList();
Vertex A = new Vertex("A");
Vertex B = new Vertex("B");
Vertex C = new Vertex("C");
Vertex D = new Vertex("D");
Vertex E = new Vertex("E");
Vertex F = new Vertex("F");
Vertex G = new Vertex("G");
Vertex H = new Vertex("H");
forest.AddVertex(A);
forest.AddVertex(B);
forest.AddVertex(C);
forest.AddVertex(D);
forest.AddVertex(E);
forest.AddVertex(F);
forest.AddVertex(G);
forest.AddVertex(H);
edges.Add(new Edge(6, A, B));
edges.Add(new Edge(3, A, D));
edges.Add(new Edge(7, A, E));
edges.Add(new Edge(4, B, C));
edges.Add(new Edge(6, B, E));
edges.Add(new Edge(3, B, F));
edges.Add(new Edge(4, B, H));
edges.Add(new Edge(3, C, F));
edges.Add(new Edge(2, D, E));
edges.Add(new Edge(6, E, F));
edges.Add(new Edge(5, E, G));
edges.Add(new Edge(5, F, H));
edges.Add(new Edge(2, G, H));
List<Edge> solution = new List<Edge>();
foreach (Edge edge in edges) {
Tree leftTree = forest.Find(edge.Left);
Tree rightTree = forest.Find(edge.Right);
if (leftTree != rightTree) {
Tree newTree = leftTree.Join(rightTree);
if (newTree == leftTree)
forest.Remove(rightTree);
else
forest.Remove(leftTree);
solution.Add(edge);
}
}
Console.WriteLine("Minimum-spanning tree is:");
foreach (Edge e in solution)
Console.WriteLine(e);
Console.ReadLine();
}
}
The really interesting bit of course is not the population of the forest or edge list, but the loop that goes through all the edges in sorted order by weight. For each edge we work out the tree that contains the left vertex and the one for the right vertex. If these are different, we join them, remove the tree that's no longer used, and add the edge to the solution.
Of course, there are some optimizations in this loop. For example, at the end of a cycle, if there is only one tree in the forest, we do not need to look at the other edges that may remain: we've already found the solution.
